Vectores

34.     La siguiente tabla muestra los valores del radio medio (R) de las órbitas de los planetas frente al período de revolución (T) en torno al Sol:

a)    Representa gráficamente R frente a T.

b)   Comprueba que la gráfica de R frente a    es una recta y calcula su pendiente.

c)    Determina el radio medio de la órbita de Saturno, cuyo período es  s.

d)   ¿Qué curva se obtiene al representar R frente a  ?

35.     Dados los vectores    y  , determina, gráficamente,  ,  y  . ¿Qué relación hay entre los vectores   y  ?

36.     El  vector     tiene  de  módulo  5 unidades  y  forma  un  ángulo  de  30⁰  con  el  semieje  X  positivo,  y el vector    forma  un  ángulo  de  45⁰  con  dicho  eje y mide 8 unidades. Dibuja ambos vectores y determina gráficamente la suma, la diferencia  , los vectores    y    y su producto escalar. Determina las componentes cartesianas de ambos vectores y realiza analíticamente los cálculos del apartado anterior.

37.     Dados los vectores de la figura, cuyos valores y direcciones se indican:

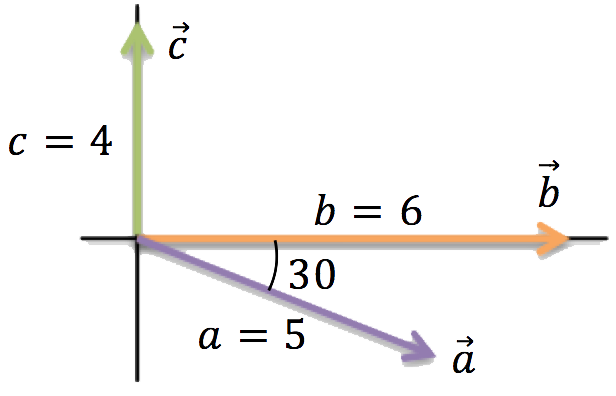a)    Calcula geométricamente la suma de los tres vectores.

b)    Determina el vector  .

c)    Obtén las componentes cartesianas de cada uno.

d)    Comprueba que se cumple: 

.

38.     Dados los vectores:  ,     y   ,  calcula:

a)    El que tiene mayor módulo.

b)   El vector que sumado a  da .

c)    Un vector unitario en la dirección de .

d)   El producto escalar de  por .

e)   El ángulo que forman  y .

39.    Dados los vectores:    y  , calcula:

a)    El módulo de cada vector.

b)   El ángulo que forman cada uno con el semieje X positivo.

c)    Su suma.

d)   La diferencia.

e)   El vector  .

f)     El producto escalar de ambos vectores.

g)    Un vector unitario en la dirección de cada uno.

40.     Dados los siguientes vectores. Calcula:

a)    Gráficamente el vector suma.

b)   Analíticamente el vector suma.

c)    El módulo del vector suma.

d)   El ángulo que forma el vector suma con respecto a la parte positiva del semieje X.

DATOS: