Galicia. Examen EBAU resuelto de Matemáticas CC.SS.. Julio 2023

PREGUNTA 3.  Análisis. El número de ejemplares vendidos de una revista (en miles de unidades), en los primeros cinco meses del año, viene dado por la función:

 

donde t es el tiempo transcurrido en meses.

 

a) Estudie el crecimiento y decrecimiento del número de ejemplares vendidos. Calcule en qué momentos se produce el máximo y el mínimo número de ventas y a cuánto ascienden.

b)  Represente gráficamente la función N(t). Calcule el área de la región delimitada por la gráfica de la función N(t), el eje de abscisas y las rectas t = 0 y t = 5.

 

 

a)  Antes  de  nada,  vamos  a  operar  el  primer  trozo  de  la  función  que  nos  dan  y  quitar  los paréntesis: 

Para calcular el crecimiento y decrecimiento de la función hacemos la primera derivada: 

 

Igualamos la derivada a cero para calcular los puntos críticos, en realidad sólo el primer trozo, porque el otro ya no tiene variable:

 

 

Miramos el signo de la primera derivada en los intervalos resultantes:

 

 

 

Vemos que las ventas de la revista aumentan el primer mes, después decrecen entre el primer y el tercer mes y, por último, del tercer al quinto año vuelven a aumentar:

 

 

 

La función tiene un máximo en t = 1, porque antes la función crece y después decrece. Para saber los valores máximos y mínimos tenemos que ver qué valores toma la función en el máximo y en los extremos de cada uno de los trozos de la función:

 

 

 

 

 

Hay un mínimo en las ventas de dicha en revista en el tercer mes con 5 000 ejemplares y un máximo en el primer y el quinto mes con 9 000 ejemplares.

 

 

b)  Representamos la función teniendo en cuenta que, el primer trozo, es una parábola y que podemos calcular el vértice de la siguiente manera:

 

 

 

El vértice está en el punto (1, 9). Con este punto y las imágenes que tenemos calculadas en el apartado anterior tenemos puntos suficientes para dibujarla. Lo mismo para el otro trozo de la función, como se trata de una recta, llega con los puntos que ya tenemos calculados.

 

 

 

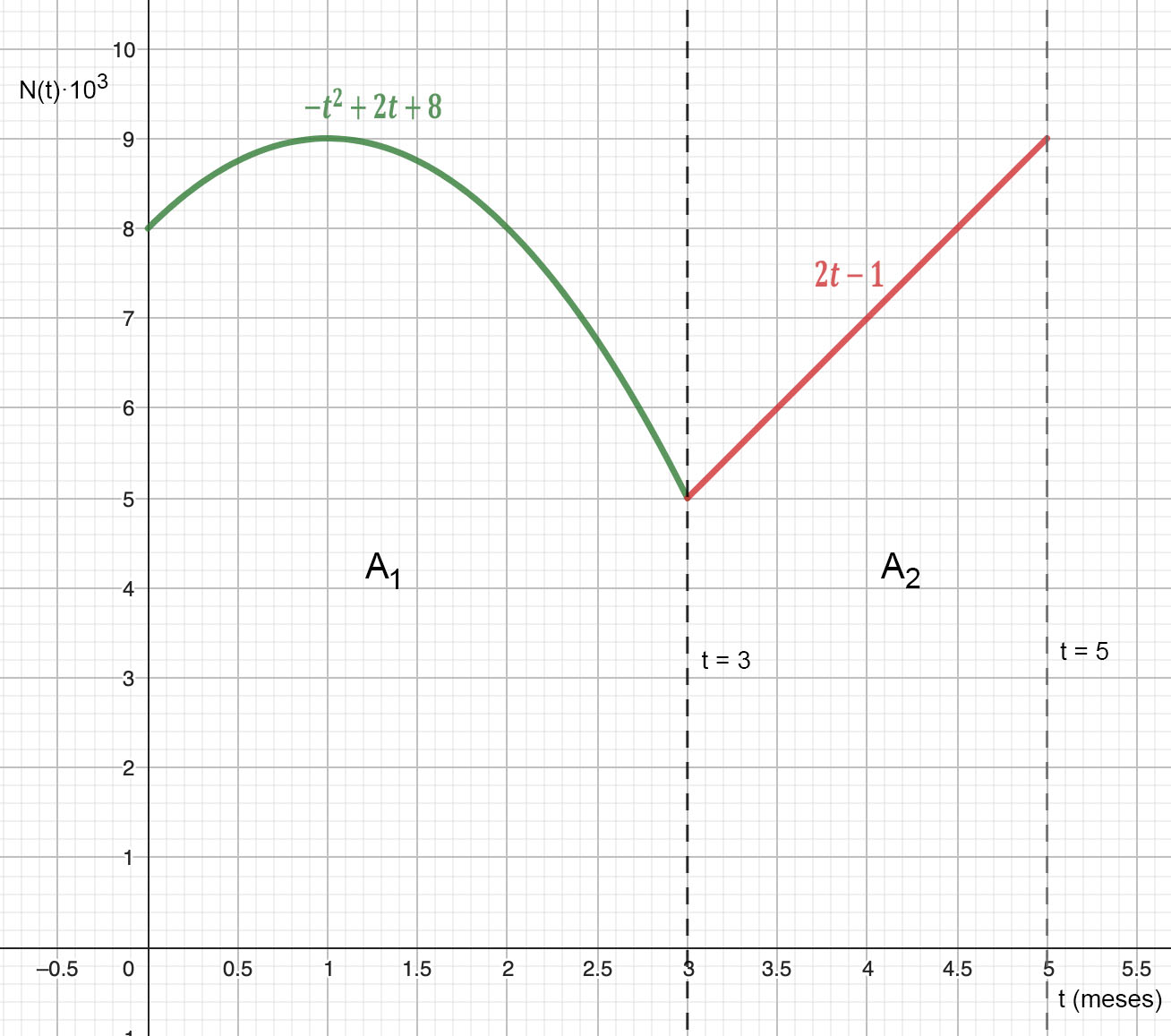
Como vemos en la gráfica anterior, el área que nos piden calcular es la que encierra la gráfica, las dos rectas verticales t = 0 (eje Y) y t = 5, y el eje X. Debemos dividirla en dos y calcular por separado la que encierra cada trozo de función. Es decir: