Galicia. Examen EBAU resuelto de Matemáticas CC.SS.. Julio 2023
PREGUNTA 2. Álgebra. Un barco pesquero se dedica a la captura de jurel y caballa. Las normas sobre cuotas son: Las capturas totales no pueden exceder de 30 toneladas (Tm); la cantidad de jurel como máximo puede triplicar la de caballa y la cantidad de caballa no puede superar las 18 Tm.
Si el precio al que vende el jurel es de 5 €/kg y el de caballa 6 €/kg.
a) Formule y resuelva el problema que determina las cantidades que debe pescar de cada especie para maximizar los ingresos, cumpliendo las normas.
b) Represente gráficamente la región factible e indique sus vértices. ¿A cuánto ascienden los ingresos máximos?
c) ¿Cumpliría las normas sobre cuotas pesqueras si captura 20 Tm de jurel y 6 Tm de caballa? Explique su respuesta.
a) Definimos:
x: número de toneladas de jurel.
y: número de toneladas de caballa.
Comenzamos por escribir las restricciones. Para ello, el enunciado nos dice que las cuotas totales no pueden exceder de 30 Tm:
![]()
También que las toneladas de jurel como máximo pueden triplicar a las de caballa:
![]()
Por último, el número de toneladas de caballa no puede superar las 18 toneladas:
![]()
Nos queda imponer una restricción más y que cuando dibujemos la región factible vamos a comprender que es necesaria y evidente:
![]()
Para escribir la función a maximizar debo tener en cuenta que x e y están en toneladas y el precio me lo dan en quilogramos. Para ponerlo en €/Tm tengo que multiplicar por 1 000:
![]()
![]()
b) Representamos el conjunto de soluciones e identificamos la región factible:
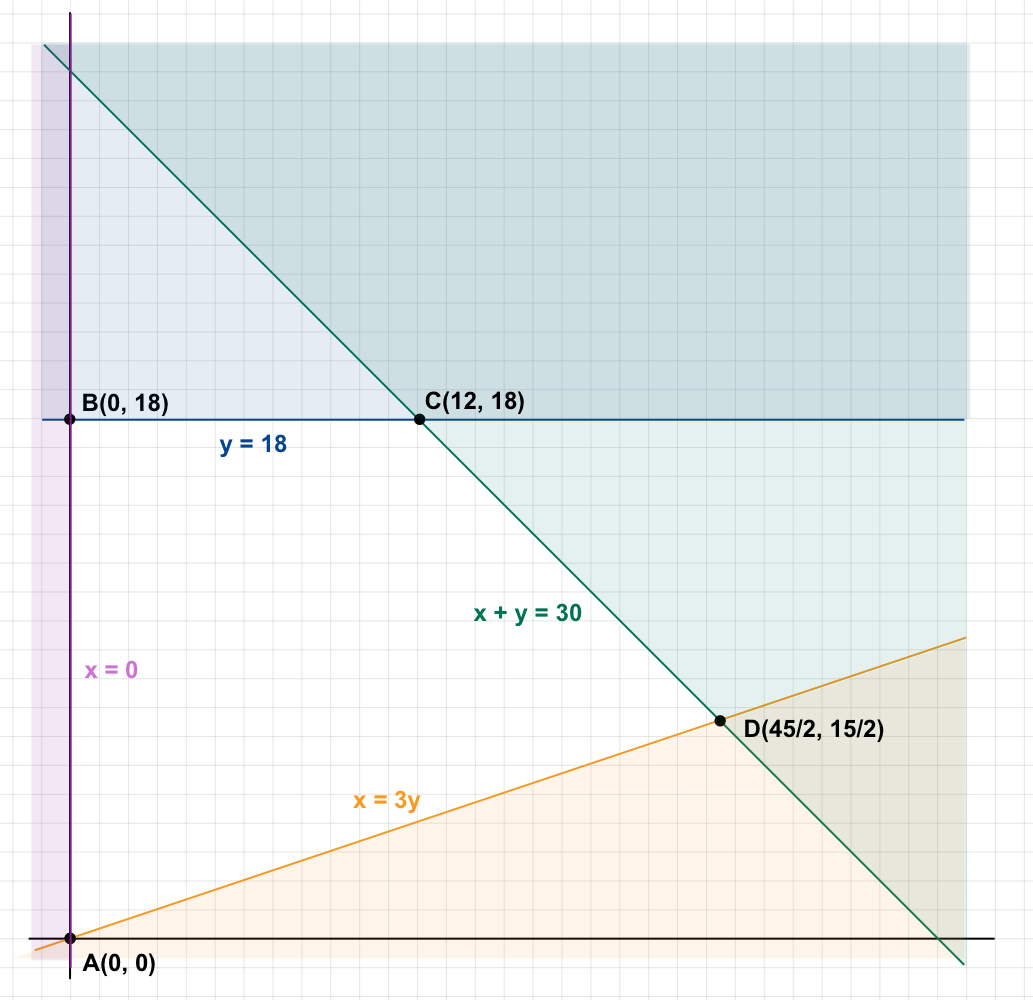
Calculamos el valor que toma en cada uno de los vértices:
![]()
![]()
![]()
![]()
La solución óptima de la función objetivo, que es la que proporciona más beneficios, es la del vértice C. Deberían capturar 12 toneladas de jurel y 18 toneladas de caballa y obtendrían unos beneficios de 168 000 €.
c) Para cumplir las normas tendría que verificar todas las restricciones propuestas y, no las cumple, porque no cumple la segunda:
![]()
Si captura 20 toneladas de jurel y 6 de caballa incumpliría las normas sobre cuotas.

