Galicia. Examen EBAU resuelto de Matemáticas II. Julio 2022

7. Estadística y Probabilidad:

a)  En una famosa biblioteca, el 70% de los libros son novelas, el 40% son clásicos anteriores al siglo XIX y el 60% de los clásicos son novelas. Si se elige en esa biblioteca un libro al azar, calcule la probabilidad de que no sea una novela, pero sí un clásico, y la probabilidad de que sea un clásico sabiendo que es una novela.

b)  En un cierto país, el 80% de los delitos contra la propiedad quedan sin resolver. Si en una localidad de ese país se cometieron 3 de esos delitos, calcule la probabilidad de que se resuelva por lo menos 1.

 

a)   Definimos los sucesos siguientes:

C = “clásicos anteriores al siglo XIX de una determinada biblioteca”

N = “novelas de una famosa biblioteca” 

El enunciado nos da la probabilidad de estos dos sucesos, además de la probabilidad condicionada de que un libro sea una novela sabiendo que se trata de un clásico:

A partir de la probabilidad total de que elegido un libro al azar sea una novela (hay novelas que son clásicos y novelas que no son clásicos), podemos calcular la probabilidad condicionada de que un libro sea una novela sabiendo que no es un clásico:

 

 

Con todas estas probabilidades podemos hacer un diagrama de árbol:

 

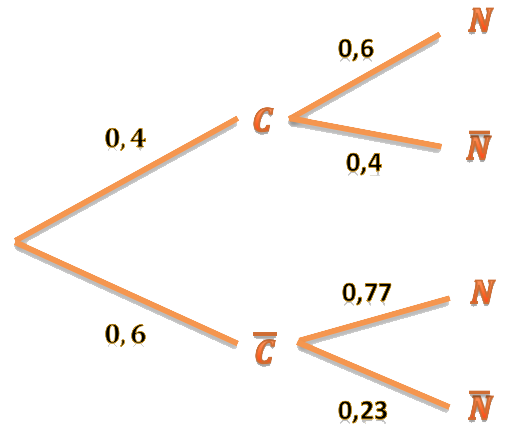
La primera de las probabilidades que nos piden es una intersección de sucesos:

La probabilidad de que elegido al azar un libro no sea una novela y sí un clásico es 0,16.

La otra probabilidad que nos piden es una probabilidad condicionada:

La probabilidad de que elegido un libro al azar sea un clásico sabiendo que es una novela es 0,34.

 

b)  Sea “X: el número de delitos contra la propiedad que se resuelven en un cierto país”. . 

La fórmula de la distribución binomial es:

 

 

La probabilidad que nos piden es que de cada 3 delitos que se cometen por lo menos que se resuelva 1. Es decir, que se podría resolver uno, dos o los tres. Por cuestión de ahorrarnos cálculo hallaremos el suceso complementario:

 

 

 

 

Así si en esa localidad de ese determinado país se cometen 3 delitos, la probabilidad de que se resuelva por lo menos 1 es de 0,488.