Galicia. Examen EBAU resuelto de Matemáticas II. Julio 2022

5. Geometría:

a)  Obtenga la ecuación implícita o general del plano  que contiene a la recta      y pasa por el punto .

b)  Calcule el punto simétrico de  con respecto al plano .

a)   Obtenemos el vector director de la recta y un punto de la misma:

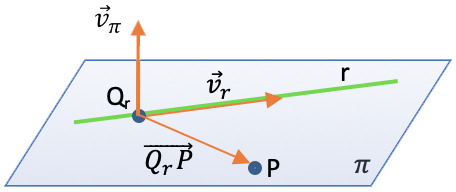
Para calcular la ecuación del plano necesitamos dos vectores (contenidos en el propio plano) y un punto. Los dos vectores los obtenemos, uno del vector director de la recta y el otro haciendo un vector que va desde un punto cualquiera de la recta, Q_r, al punto P por el que tiene que pasar el plano:

b)  Para calcular el punto simétrico del punto  respecto del plano    vamos a calcular una recta s, perpendicular al plano que pase por el punto P. Por lo tanto, el vector director de esa recta llevará la misma dirección que el vector normal del plano:

Ahora vamos a calcular el punto M, es decir, el punto donde esta recta corta al plano. Para ello substituimos las ecuaciones paramétricas de la recta en el plano:

Con el valor del parámetro calculamos el punto sustituyéndolo en las ecuaciones paramétricas de la recta:

Este punto es el punto medio entre el punto P y su simétrico, P’: