Galicia. Examen EBAU resuelto de Matemáticas II. junio 2022

5. Geometría:

a)  Obtenga la ecuación implícita o general del plano  que pasa por el punto  y es perpendicular a la recta .

b)  Calcule los puntos de la recta , cuya distancia al plano  es igual a 2.

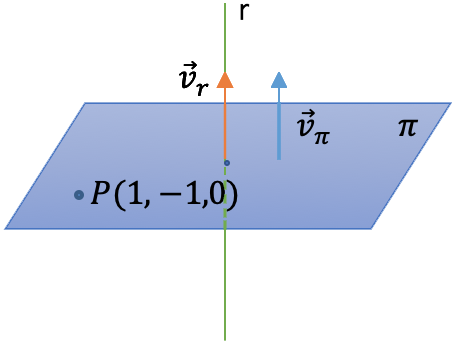
a)   Como la recta es perpendicular al plano, el vector director de la recta es el vector normal del plano. Como además tenemos un punto del plano, podemos determinar la ecuación implícita o general que nos piden:

b)  Cogeremos un punto genérico de la recta y, para eso, las coordenadas de ese punto van a ser las propias ecuaciones paramétricas: .

Después hacemos que la distancia de ese punto genérico al plano sea igual 2 unidades:

Resolvemos:

Para calcular los puntos que distan 2 unidades del plano, sólo debemos substituir los valores del parámetro en la recta r: