Galicia. Examen EBAU resuelto de Matemáticas II. junio 2022

3. Análisis:

a)  Calcule los límites    y  , donde  es el logaritmo neperiano de x.

b)  Dibuje la gráfica de una función f continua y no negativa en el intervalo  tal que: , ,    en el intervalo  ,    en el intervalo   y f es constante en el intervalo  .

a)   El primer límite presenta una indeterminación que resolvemos por L’Hôpital:

El segundo de los límites presenta una indeterminación que podemos transformar fácil en otra que resolvemos por la regla de L’Hôpital:

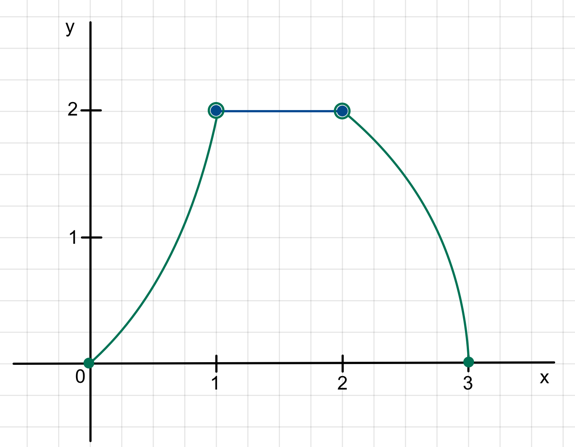
b)  Tenemos que dibujar una función en el intervalo , de forma que las imágenes de los extremos son cero y que la gráfica de la misma tiene que estar por encima del eje X, ya que no puede ser negativa. La función deberá tener tres trozos o intervalos:

·   En este intervalo  la función tiene que ser creciente (no puede descender y ser negativa). Podemos escoger hasta donde va a subir la función. Admite infinitas soluciones. En este ejemplo pusimos . Como nos dicen que la segunda derivada es positiva, la función tiene que ser convexa.

·   En el intervalo  la función es constante y por lo tanto una recta horizontal.

·   En el último tramo,  tiene que volver a ser decreciente porque . Pero como la segunda derivada en este tramo es negativa, la función debe ser cóncava.

El  último  dato  a  tener  en  cuenta  es  que  la  función  es  continua, por lo que la función en el punto x =1 y x = 2 debe comenzar donde terminaba el tramo anterior.