Galicia. Examen EBAU resuelto de Matemáticas CC.SS.. junio 2022

PREGUNTA 4. Análisis. Dada la función  .

a)  Calcule el valor del parámetro “a” teniendo en cuenta que la función f(x) presenta un punto de inflexión en .

b)  Para , calcule el área del recinto limitado por la gráfica de la función f(x) y el eje OX.

a)   Los puntos de inflexión son los valores que anulan la segunda derivada de la función. Calculamos entonces las dos primeras derivadas:

Aplicando la condición antes mencionada nos queda:

b)  La función nos queda de la siguiente manera:

Hacemos un esbozo de la gráfica para identificar el área o áreas a calcular. Para eso calculamos los puntos de corte con el eje X:

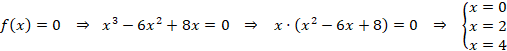
Con los puntos de corte y dando valores para saber por dónde va la función hacemos la gráfica:

En el dibujo identificamos las áreas que tenemos que calcular (sombreadas en verde). Como vemos son las dos iguales, con lo que el área total será el doble de cada una de ellas.

Planteamos la integral para calcular la primera. Para eso integramos la función que encierra el área entre los valores 0 y 2:

Como dijimos antes el área total es el doble, por lo que, el área del recinto limitado por la gráfica de la función f(x) y el eje OX es de 8 u².