Galicia. Examen EBAU resuelto de Matemáticas CC.SS.. junio 2022

PREGUNTA 3.  Análisis. En una zona protegida de un parque natural el número de aves N(t), en cientos, en función del tiempo t (años transcurridos desde que se contabilizan las aves) viene dado por la función:

 

 

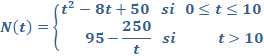
a)  Calcule los intervalos de crecimiento y decrecimiento de la función N(t) ¿Entre qué años crece la función? ¿Entre qué años decrece?

b)  ¿Cuándo se alcanza el número mínimo de aves en el parque? ¿Cuántas aves hay en ese momento?

c)   Calcule el intervalo de tiempo en el que la población de aves se mantiene entre 5 000 y 7 500 aves. ¿A qué valor tiende la población de aves con el paso del tiempo?

 

a)   Para calcular el crecimiento y decrecimiento de la función hacemos la primera derivada:

 

 

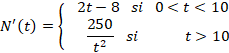
Igualamos la derivada a cero para calcular los puntos críticos:

 

 

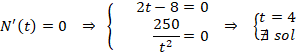
Miramos el signo de la primera derivada en los intervalos resultantes:

 

 

 

 

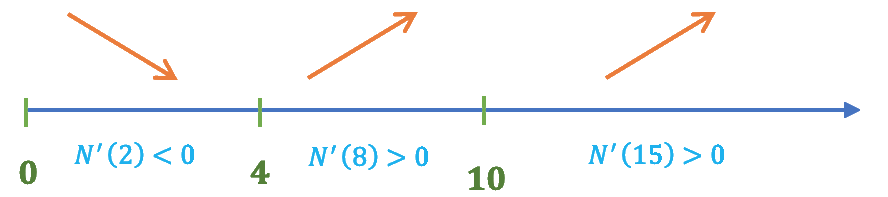
La función decrece los primeros 4 años y de ahí en adelante es siempre creciente.

 

 

b)  La función tiene un mínimo en el cuarto año, porque antes de ese instante la función decrece y a partir de ahí crece. Calculamos el número de aves en ese cuarto año:

 

 

En el cuarto año se alcanza el número mínimo de aves en el parque y, en ese momento, hay 3 400 aves.

 

 

c)   Para poder responder deberemos resolver la siguiente inecuación:

 

 

Como es una función por partes, deberemos hacerlo con los dos trozos de la función. Con el primero nos queda:

 

 

 

Si igualamos a cero cada una de esas dos inecuaciones y resolvemos nos queda:

 

 

Las dos últimas soluciones no nos valen pues están fuera del intervalo de existencia de este trozo de la función. Las dos primeras sí son válidas y vemos que entre los 0 y los 8 años el número de aves es inferior a 5 000 y entre los 8 y los 10 años ya es mayor de esa cantidad y menor de 7 500:

 

 

 

Como ya vimos en el apartado anterior, a partir del cuarto año, aumenta siempre el número de aves. Sólo tenemos que calcular entonces en qué momento se alcanza una población de 7 500 aves:

 

 

Por lo tanto, la población de aves se encuentra entre las 5 000 y las 7 500 entre (8; 12,5) años.

 

Para saber a donde tiende la función y, por lo tanto, el número de aves tenemos que calcular el límite cuando el tiempo tiende a infinito. Lo hacemos con el segundo trozo de la función, puesto que es en él donde calculamos los valores mayores a 10:

 

 

Con el paso del tiempo la población de aves tiende a 9 500 aves.