Galicia. Examen EBAU resuelto de Matemáticas II. Junio 2018

1.    

a)  Discute, según los valores del parámetro m, el sistema de ecuaciones: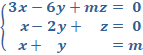

b)  Resuélvelo, si es posible, cuando .

a)  Planteamos dos matrices, la de coeficientes (A) y la ampliada con los términos independientes (A^*):

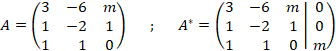
Calculamos el determinante de la matriz A para determinar su rango:

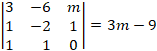
Igualamos a cero el determinante para saber qué valores de m lo anulan:

El rango de la matriz A será:

·   Si  .

·   Si  , ya que encontramos algún determinante de este orden distinto de cero:

Los casos que tenemos entonces serían los siguientes:

·   Si 

El rango de la matriz ampliada es 3, porque el determinante de A, que era distinto de cero, también está en la matriz ampliada.

·   Si 

   El rango de la matriz ampliada también es 2, porque todos los determinantes de orden 3 son nulos.

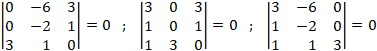
b)  Para el caso de m = 3, el sistema es compatible indeterminado, por lo tanto, una de las ecuaciones es combinación lineal de las otras. Si multiplicamos la segunda ecuación por tres obtenemos la primera. Por lo tanto, podemos eliminar esa primera ecuación por ser combinación lineal de la segunda:

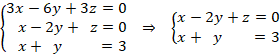
Ahora ponemos una incógnita como parámetro, por ejemplo,    y resolvemos: