Galicia. Examen EBAU resuelto de Matemáticas II. Junio 2018

4.   En las rebajas de unos grandes almacenes están mezcladas y a la venta 200 bufandas de la marca A, 150 de la marca B y 50 de la marca C. La probabilidad de que una bufanda de la marca A sea defectuosa es 0,01; 0,02 si es de la marca B y 0,04 si es de la marca C. Una persona elige una bufanda al azar:

a)  Calcula la probabilidad de que la bufanda elegida sea de la marca A o defectuosa.

b)  Calcula la probabilidad de que la bufanda elegida no sea defectuosa ni de la marca C.

c)   Si la bufanda elegida no es defectuosa, ¿cuál es la probabilidad de que sea de la marca B?

 

a)   Definimos los sucesos siguientes y sus probabilidades:

A = “elegir una bufanda de la marca A”, 

B = “elegir una bufanda de la marca B”,

C = “elegir una bufanda de la marca C”,

D = “elegir una bufanda que sea defectuosa”

Con estos sucesos y con los datos del problema podemos hacer un diagrama de árbol:

  

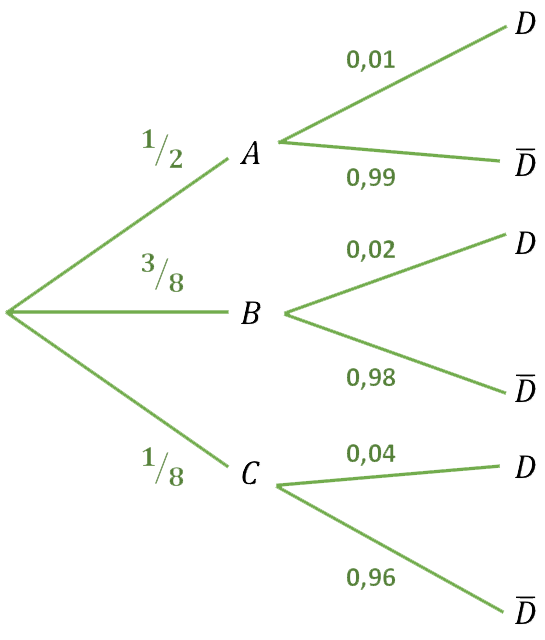
Lo primero, vamos a calcular la probabilidad total de que, al elegir al azar una bufanda esta sea defectuosa:

Nos pide una unión de sucesos, que sea de la marca A o defectuosa:

La probabilidad de que la bufanda elegida sea de la marca A o sea defectuosa es 0,51.

 

b)  Una de las maneras de resolver este apartado es utilizar una de las leyes de Morgan:

Vamos a calcular la unión de los sucesos D y C, de manera análoga a como hicimos en el apartado anterior:

Sería la probabilidad de que la bufanda elegida sea de la marca C o sea defectuosa. Calculamos el suceso contrario:

Ahora aplicando la ley de Morgan obtenemos el suceso pedido:

La probabilidad de que la bufanda elegida no sea defectuosa ni de la marca C es 0,86.

 

c)   Vamos a calcular la probabilidad de que la bufanda elegida no sea defectuosa:

Lo que nos piden ahora es una probabilidad condicionada:

La probabilidad de que la bufanda elegida sea de la marca B, sabiendo que no es defectuosa es 0,37.