Galicia. Examen EBAU resuelto de Matemáticas II. Junio 2018

3.    

a)  Determina  el  valor  de    para  que  los  puntos  ,  ,    y  sean coplanarios y calcula la ecuación implícita o general del plano que los contiene.

b)  Determina la posición relativa del plano   y la recta r que pasa por los puntos   y  . Si se cortan, calcula el punto de corte.

c)  Calcula el punto simétrico del punto  respecto del plano .

 

a)   Vamos a empezar calculando dos vectores:

 

Para calcular un plano necesitamos tres puntos que no estén alineados. Por lo tanto, vamos a calcular la ecuación implícita de un plano que contenga los puntos A, B y C. Para eso necesitamos un punto del plano, el A por ejemplo, y dos vectores del propio plano: 

Podemos simplificar la ecuación del plano y nos quedará:

Si los cuatro puntos son coplanarios, el punto D tiene que pertenecer al plano formado por los otros 3 puntos. Es decir, el punto D tiene que estar contenido en el plano que acabamos de calcular. Sabiendo eso calculamos el valor del parámetro:

 

b)  Vamos a calcular las ecuaciones paramétricas de la recta. Para eso necesitamos el vector director: 

La recta nos quedará: 

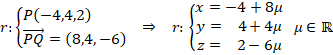
Para calcular la posición relativa de la recta y el plano, sustituimos las ecuaciones paramétricas de la recta en la ecuación implícita del plano y resolvemos:

Al obtener un valor del parámetro, la recta r y el plano  son secantes. Para calcular el punto de corte solo tenemos que sustituir el valor del parámetro en las ecuaciones paramétricas de la recta:

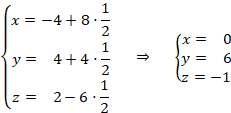
El punto de intersección será el .

 

c)  Para calcular el punto simétrico del punto  respecto del plano    vamos a calcular una recta s, perpendicular al plano que pase por el punto P. Por lo tanto, el vector director de esa recta llevará la misma dirección que el vector normal del plano:

 

 

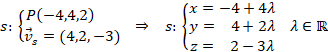
En realidad, esta recta es la misma que la del apartado anterior, r. Es decir, que la recta r no sólo es secante al plano, si no que además es perpendicular. Eso quiere decir que el punto donde la recta corta al plano, M, es el punto de intersección que también tenemos hallado. De todas formas, vamos a comprobarlo. Para ello substituimos las ecuaciones paramétricas de la recta en el plano:

 

 

Con el valor del parámetro calculamos el punto sustituyéndolo en las ecuaciones paramétricas de la recta:

 

 

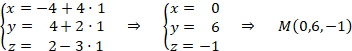
Como vemos es el punto que ya teníamos. Este punto es el punto medio entre el punto P y su simétrico, P’: