Galicia. Examen PAU resuelto de Matemáticas CC.SS.. Junio 2015

2.    Consideremos la función  .

(a)    Calcula el valor de “a” y de “b” sabiendo que la función f(x) tiene un extremo relativo en el punto  .

(b)   Suponiendo que    y  , determina, clasificándolos, los extremos relativos de la función f(x).

(a)      Si la función tiene un extremo relativo en el punto    se cumple que  :

Obtenemos una ecuación con dos incógnitas. Podemos obtener otra, porque ese punto es de la función y por lo tanto cumple que:

Con estas dos ecuaciones resolvemos el sistema y calculamos los valores de a y de b:

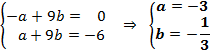
(b)     Para eses valores de a y de b la función quedaría así:

Y la primera derivada:

Igualamos a cero, para calcular los puntos críticos:

Hacemos la segunda derivada y substituimos los puntos críticos en la misma para saber si son máximos o mínimos relativos:

Calculamos la ordenadas de los extremos relativos:

La función tiene un mínimo relativo en el punto  y un máximo relativo en el punto .