Galicia. Examen PAU resuelto de Matemáticas CC.SS.. Septiembre 2013

1)   El dueño de una tienda de fotografía desea comercializar dos tipos de cámaras de fotos A y B con un precio de venta al público de 210 y 300 euros la unidad, respectivamente. Para la compra de ambos tipos dispone de un máximo de 2760 euros y hará el pedido a un almacén que le cobra 120 euros por cada cámara del tipo A y 180 euros por cada cámara del B. El dueño hará el pedido con la condición de que: al menos 3 cámaras sean del tipo A, entre 4 y 12 sean del B y el número de cámaras del tipo A no debe superar en más de tres unidades al número de cámaras del tipo B.

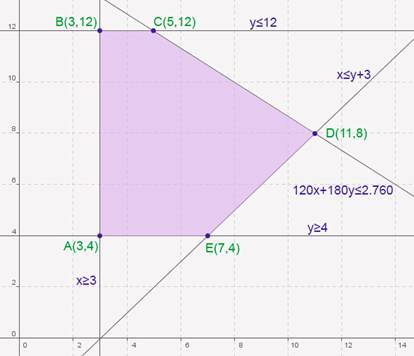
(a)     Formula el sistema de inecuaciones asociado al problema. Representa la región factible y calcula sus vértices.

(b)  ¿Cuántas cámaras de cada tipo deberá adquirir para que los beneficios obtenidos sean máximos?

(a)     x: número de cámaras del tipo A

y: número de cámaras del tipo B

  Los vértices se calculan:

    ⇒       ;        ⇒          ;         ⇒  

    ⇒        ;         ⇒  

(b)      Necesitamos la función objetivo, que en este caso nos debe dar los beneficios:

Para saber cuántas cámaras debe vender para maximizar los beneficios, sustituimos cada uno de los vértices en la función objetivo:

A ⇒  

B ⇒

C ⇒  

D ⇒    ⇒  Alcanza el máximo

E  ⇒

Por lo tanto, deberá vender 11 cámaras del tipo A y 8 cámaras del tipo B, para obtener un beneficio de 1 950 €