Galicia. Examen EBAU resuelto de Matemáticas II. Junio 2017

2.    

a)  Calcula   

 

b)  Se desea construir una caja de base cuadrada, con tapa y con una capacidad de 80 dm³. Para la tapa y la superficie lateral se quiere utilizar un material que cuesta 2 €/dm² y para la base otro que cuesta 3 €/dm². Calcula las dimensiones de la caja para que su coste sea mínimo.

c)   Calcula  .

 

a)  Resolvemos el límite propuesto aplicando la regla de L’Hôpital, derivando el numerador y el denominador, para la indeterminación 0/0:

 

 

 

 

El resultado del límite es:

 

 

 

b)  Para resolver este problema de optimización, debemos plantear una función que nos dé el coste de la caja. Esta función será:
 

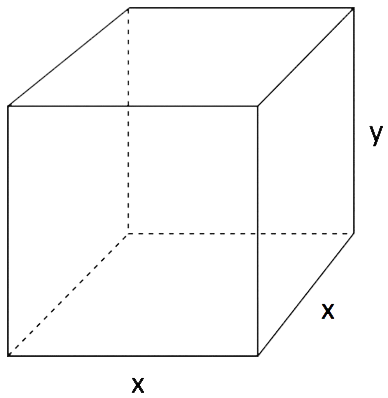
Esta función depende de dos variables, para ponerla solo en función de una, vamos a utilizar el dato del volumen de la caja:

 

Volvemos a la función del coste y sustituimos, obteniendo así el coste en función sólo de una variable:

 

Ahora tenemos que calcular los máximos y mínimos. Para eso hacemos la primera derivada e igualamos a cero:

 

Una vez obtenido el punto crítico debemos saber si es un máximo o un mínimo, para eso vamos a hacer la segunda derivada:

Sustituimos el punto crítico en la segunda derivada: 

 

Sabemos que para ese valor el coste de la caja es mínimo. Tan sólo nos queda calcular la altura:

 

Las dimensiones de la caja para que el coste de esta sea mínimo son de 4 dm el lado de la base y 5 dm la altura.

 

c)   La integral propuesta vamos a resolverla por partes:

 

La fórmula sería:

 

La integral quedaría:

 

 

 

Llegamos a una integral racional en la que el numerador es mayor que el denominador, por lo que podemos dividir:

 

Aplicando la regla de la división:

 

 

Por lo tanto, la integral nos quedará:

 

 

Una vez resuelta la integral indefinida, ahora vamos a resolver la definida:

 

 

El resultado final de la integral será: